PythonData Science

Matplotlib Animation

, , ,
  • 정지된 그림으로는 볼 수 없는 것들이 있습니다.
  • 시간에 따른 변화나 입체 도형의 뒷면이 그것입니다.
  • 애니메이션을 활용해 이를 보완합니다.

1. Matplotlib animation

matplotlib.animation

  • Matplotlib에서 사용할 수 있는 애니메이션은 두 가지가 있습니다.
  • Artist 객체 변화를 저장하는 ArtistAnimation,
  • Figure 전체의 변화를 저장하는 FuncAnimation이 그 것입니다.

1.1. base figure

  • 간단한 그림을 그려서 애니메이션으로 만듭니다.
  • 가운데 동그라미를 하나 그리고, 이 동그라미가 점점 커지는 모습을 구현합니다.
  • 기본 명령어를 사용해 화면 한가운데 동그라미를 그립니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# 기본 설정
%matplotlib inline

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd

sns.set_context("talk")
sns.set_style("ticks")
sns.set_palette("colorblind")

# 가운데 동그라미 점 하나
fig, ax = plt.subplots(figsize=(5, 5), constrained_layout=True)
ax.set(xlim=(-1, 1), ylim=(-1, 1), xticks=[], yticks=[])

circle = ax.scatter(0, 0, s=10, lw=1, ec="b", fc="none")


  • 객체 지향 방식을 사용해 이 객체의 크기를 바꾸겠습니다.
  • circle이라는 이름으로 저장한 marker 하나는 collections로 다루어집니다.
  • .set_sizes()에 list 형태로 새로운 size를 전달하여 크기를 변경합니다.
  • marker가 하나밖에 없으므로 원소가 하나뿐인 list를 입력합니다.
  • 이를 update()라는 이름의 함수로 만들어 적용합니다.
1
2
3
4
5
6
7
8
9
# marker 크기 변경 함수
def update(frame_number):
    circle.set_sizes([frame_number*30])

# marker 크기
update(10)

# 화면 출력
display(fig)


  • 화면 가운데 있는 원이 커졌습니다.
  • 이제 연속적으로 적용하고 .gif 파일로 적용하면 애니메이션이 됩니다.

1.2. FuncAnimation

matplotlib.animation.FuncAnimation

  • frame마다 변하는 Figure 차례로 저장해 애니메이션으로 만듭니다.
  • Figure 객체에 위에서 만든 update()같은 함수를 연속적으로 적용합니다.
  • 이 때 사용하는 함수가 FuncAnimation이고, Figure 객체, 함수와 함께 frames에 총 프레임을 넣고,
  • intervals에 frame 사이 시간 간격을 ms단위로 입력합니다.
  • 위 두 코드 뒤에 FuncAnimation 한 줄을 추가하고, .save()로 파일로 저장합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
from matplotlib.animation import FuncAnimation

fig, ax = plt.subplots(figsize=(5, 5), constrained_layout=True)

# Axes 주변부 요소 삭제
ax.set(xlim=(-1, 1), ylim=(-1, 1), xticks=[], yticks=[])

# scatter marker 생성
circle = ax.scatter(0, 0, s=10, lw=3, ec="b", fc="none")

# animation frame마다 적용되는 변화
def update(frame_number):
    # size 변경
    circle.set_sizes([frame_number*500])                    

# animation 객체 생성
anim = FuncAnimation(fig, update, frames=120, interval=5)

# animation을 gif로 저장
anim.save("FuncAni0.gif", fps=24)


1.3. ArtistAnimation

matplotlib.animation.ArtistAnimation

  • 조금 다른 방식으로 artist 객체의 변화를 저장해 animation을 만들 수 있습니다.
  • Artist에 변화를 준 내용을 list로 저장해서 ArtistAnimation()에 전달하는 방식입니다.
  • FuncAnimation()에는 함수를 전달했던 것과 다른 방식입니다.
  • 함수로 표현하기 어려운 급격한 변화도 담을 수 있지만 리스트가 담길 메모리는 다소 부담이 됩니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from matplotlib.animation import ArtistAnimation

fig, ax = plt.subplots(figsize=(5, 5), constrained_layout=True)

# Axes 주변부 요소 삭제
ax.set(xlim=(-1, 1), ylim=(-1, 1), xticks=[], yticks=[])

# animation frame마다 적용되는 변화
circles = []
for frame_number in range(120):
    # scatter marker 생성
    circle = ax.scatter(0, 0, s=10, lw=3, ec="b", fc="none")

    # size 변경
    circle.set_sizes([frame_number*500])                    

    # artist list 추가
    circles.append([circle])

# animation 객체 생성
anim = ArtistAnimation(fig, circles, interval=5)

# animation을 gif로 저장
anim.save("ArtistAni0.gif", fps=24)


  • 같은 애니메이션을 구현했습니다.

2. 3D 도형 시각화 적용

2.1. z axis 주변 회전

  • 원래의 목적인 3D 도형의 뒷면을 보여주는 시각화를 수행합니다.
  • Matplotlib 공식 홈페이지에 있는 구조를 가져와 다른 방식으로 그립니다.
  • Axes.contourf()를 3D Axes에 표현해보고,
  • 다른 공간에는 Axes.plot_surface()와 함께 아래 면을 사용합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# 2D mesh grid
xx, yy = np.mgrid[-2:2:20j, -2:2:20j]
zz = xx*np.exp(-(xx)**2-yy**2)

# 3D visualization
fig, axs = plt.subplots(ncols=2, figsize=(10, 7), constrained_layout=True, 
                        subplot_kw={"projection":"3d"})

# (A): filled 3D contour
axs[0].contourf(xx, yy, zz, cmap="inferno", levels=10)

# (B): 3D surface plot + 2D contour
axs[1].plot_surface(xx, yy, zz, cmap="inferno", ec="k", linewidths=0.5)
axs[1].contourf(xx, yy, zz, zdir="z", offset=-0.6)
axs[1].contour(xx, yy, zz, zdir="z", offset=-0.6, linewidths=2, colors=["w"])

titles = ["(A): Axes.contourf()", "(B): Axes.plot_surface() + 2D contours"]
for ax, title in zip(axs, titles):
    ax.view_init(azim=225, elev=20)
    ax.set_zlim(-0.6, 0.5)
    ax.set_title(title, pad=0)


  • 제법 멋진 그림이 그려졌지만 뒷부분이 보이지 않습니다.
  • 한 frame에 2도씩, 두 그림 모두 회전시킵니다. 180 frame을 적용해 한바퀴를 돌립니다.
1
2
3
4
5
6
7
8
9
10
# animation frame마다 적용되는 변화
def update(frame_number):
    axs[0].view_init(azim=225 + frame_number*2)
    axs[1].view_init(azim=225 + frame_number*2)

# animation 객체 생성
anim = FuncAnimation(fig, update, frames=180, interval=5)

# animation을 gif로 저장
anim.save("FuncAni1.gif", fps=24)


  • 빙글빙글 돌아가는 모습이 표현됩니다.

2.2. 3D 회전

Pega Devlog: 3D curved surfaces

  • 이번에는 조금 더 자유롭게 회전시켜보겠습니다.

  • Axes.view_init()에 들어가는 두 개의 인자, elev와 azim에 랜덤으로 만든 array를 입력하면 됩니다.

  • 돌려보는 재미가 있는 3D 객체를 생성합니다. 오른쪽 Ni 그림을 사용합니다.

  • 과거 글에 있는 그림을 사용합니다.

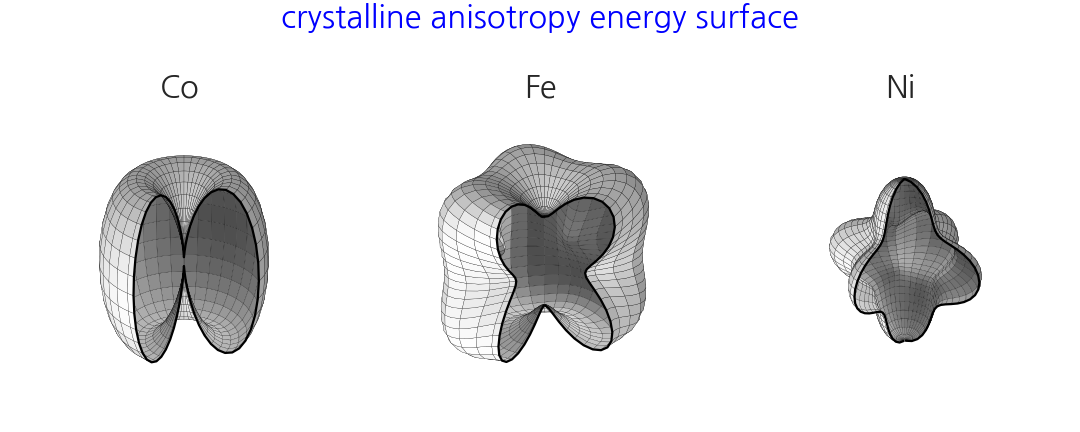
  • 핵심 코드만 가져옵니다.

  • 잘려진 부분 없이 온전한 모습으로 그립니다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
from itertools import product
from matplotlib.colors import LightSource

# angles
polars = np.linspace(0, 179, 37)
azimuths = np.linspace(0, 360, 73)

df = pd.DataFrame(product(polars, azimuths), columns=["azi", "polar"])
df["x"] = df.apply(lambda x: np.cos(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
df["y"] = df.apply(lambda x: np.sin(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
df["z"] = df.apply(lambda x: np.cos(np.deg2rad(x[0])), axis=1)

# 3D 객체 생성
K1_Ni = -0.5 
K2_Ni = -0.2
def calc_uni(K1, K2, df):
    return K1*(df["x"]**2 + df["y"]**2)

def calc_cubic(K1, K2, df):
    return K1*(df["x"]**2 * df["y"]**2 + \
               df["y"]**2 * df["z"]**2 + \
               df["z"]**2 * df["x"]**2) + \
           K2*(df["x"]**2 * df["y"]**2 * df["z"]**2)

df["E_Ni"] = df.apply(lambda x: calc_cubic(K1_Ni, K2_Ni, x), axis=1)*3 +1

# 극좌표계를 직교좌표계로 변환
df["x_Ni"] = df["E_Ni"] * df["x"]
df["y_Ni"] = df["E_Ni"] * df["y"]
df["z_Ni"] = df["E_Ni"] * df["z"]

fig, ax = plt.subplots(figsize=(5, 5), constrained_layout=True,
                       subplot_kw={"projection": "3d"})
ax.plot_surface(df[f"x_Ni"].values.reshape((37, 73)), 
                    df[f"y_Ni"].values.reshape((37, 73)), 
                    df[f"z_Ni"].values.reshape((37, 73)), 
                    ec="k", lw=0.2,
                    color="w", lightsource=LightSource(0, 10))

ax.set_box_aspect((1, 1, 1))
elev0, azim0 = 20, -60
ax.view_init(elev0, azim0)
ax.axis(False)


  • elev와 azim을 미리 array로 만들어 두고,
  • frame_number를 index로 사용해 하나씩 꺼내는 함수를 만듭니다.
  • 그리고, FuncAnimation()에서 이들을 호출해 애니메이션을 생성합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
frames = 360
elev = elev0 + np.random.normal(loc=3, scale=1, size=frames).cumsum()
azim = azim0 + np.random.normal(loc=3, scale=1, size=frames).cumsum()

# animation frame마다 적용되는 변화
def update(frame_number):
    ax.view_init(elev[frame_number],
                 azim[frame_number])

# animation 객체 생성
anim = FuncAnimation(fig, update, frames=360, interval=5)

# animation을 gif로 저장
anim.save("FuncAni2.gif", fps=24)


  • 3차원 공간을 자유롭게 회전하는 영상이 되었습니다.


도움이 되셨나요? 카페인을 투입하시면 다음 포스팅으로 변환됩니다

Share