PythonData Science

3D curved surfaces

, ,
  • 자주 있는 일은 아니지만 3차원 곡면을 그릴 때가 있습니다.
  • 어떤 분은 원자를 표현하느라, 또는 쇠구슬을 표현하느라 구가 필요할지도 모릅니다.
  • 저는 업무상 태양이 하늘에 떠 있는 지점을 고민할 때가 많아서 반구가 필요합니다.
  • 과거에는 원자의 3차원 에너지를 표현하느라 이런 그림이 필요했습니다.

1. 데이터 준비

wikipedia: Spherical coordinate system

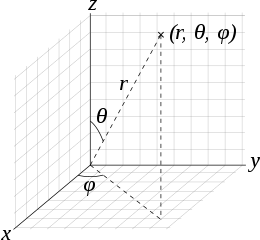
wikipedia: 구면 좌표계

  • 구나 반구를 그리려면 구면 좌표계로 정의된 데이터가 필요합니다.
  • 간단한 삼각함수를 사용해서 구면 데이터를 만듭니다.
  • 방위각(azimuthal angle, $\theta$)과 극고도각(polar angle, $\varphi$)을 나열한 뒤 여기에 아래 수식을 적용합니다.

$$
\begin{aligned}
x &= r \cos{\varphi} \sin{\theta}\\
y &= r \sin{\varphi} \sin{\theta}\\
z &= r \cos{\theta}
\end{aligned}$$

  • 코드로는 이렇게 정리됩니다.
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    # angles
    polars = np.linspace(0, 180, 19)
    azimuths = np.linspace(0, 360, 37)

    # points
    from itertools import product

    df = pd.DataFrame(product(polars, azimuths), columns=["azi", "polar"])
    df["x"] = df.apply(lambda x: np.cos(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
    df["y"] = df.apply(lambda x: np.sin(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
    df["z"] = df.apply(lambda x: np.cos(np.deg2rad(x[0])), axis=1)

    df
    • 실행 결과

2. 3D 곡면 도형 그리기

matplotlib: 3D surface (colormap)
matplotlib: mpl_toolkits.mplot3d.axes3d.Axes3D

  • 주어진 데이터로 만들어지는 3D 표면 형상을 만드는데는 .plot_surface()가 적격입니다.
  • 앞서 만든 데이터로 구(sphere)와 반구(hemisphere)를 만들어봅시다.

2.1. sphere

  • 우리가 만든 좌표가 이미 구의 좌표입니다.

  • 방위각 $\varphi$를 0도에서 360도, 극고도각 $\theta$를 0도에서 180도까지 변화시켰고, 이는 3차원 공간의 모든 방향에 해당되기 때문입니다.

  • 그렇다면 남은 일은, DataFrame에 1차원으로 들어있는 각각의 좌표를 차원에 맞게 2차원으로 바꿔주는 것 뿐입니다.

  • 극고도각과 방위각의 경우의 수가 각각 19가지, 37가지이므로 .reshape((19, 37)을 적용합니다.

  • matplotlib은 구면좌표계가 아니라 직교좌표계를 사용합니다. x, y, z로 변환합니다.

    1
    2
    3
    4
    5
    6
    fig, ax = plt.subplots(figsize=(5, 5), 
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37)), 
                    df["y"].values.reshape((19, 37)), 
                    df["z"].values.reshape((19, 37)), 
                    alpha=0.3)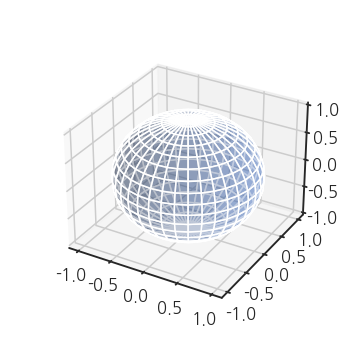


  • 구가 그려졌습니다.

  • 그런데 z축 방향으로 조금 찌그러져서 납작한 느낌이 나네요.

  • aspect ratio를 1:1:1로 맞춰줍시다.

  • matplotlib 3차원 Axes(Axes3D)에서 aspect ratio를 지정하는 명령은 .set_box_aspect()입니다.

    1
    2
    3
    4
    5
    6
    7
    fig, ax = plt.subplots(figsize=(5, 5), 
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37)), 
                    df["y"].values.reshape((19, 37)), 
                    df["z"].values.reshape((19, 37)), 
                    alpha=0.3)
    ax.set_box_aspect((1, 1, 1))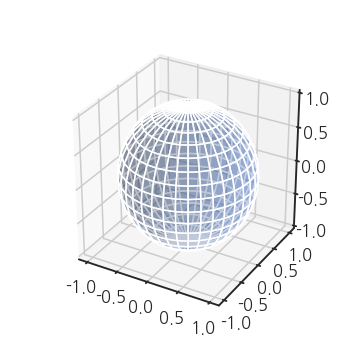


2.2. partial sphere

  • 극좌표계를 사용해서 구의 일부를 쪼개볼 수도 있습니다.
  • plot_surface()안에 넣는 x, y, z에다 slicing을 추가하면 됩니다.
  • 극고도각은 전체 범위를 사용하고 방위각은 마지막 9개를 사용하지 않겠다고 하면 이런 그림이 그려집니다.
    1
    2
    3
    4
    5
    6
    7
    fig, ax = plt.subplots(figsize=(5, 5), 
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37))[:,:-9], 
                    df["y"].values.reshape((19, 37))[:,:-9], 
                    df["z"].values.reshape((19, 37))[:,:-9], 
                    alpha=0.3)
    ax.set_box_aspect((1, 1, 1))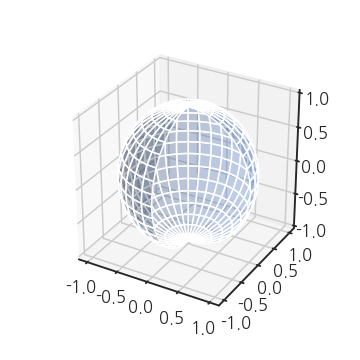

2.3. 선 색깔 조정

  • 우리는 지금 면을 그리고 있습니다.

  • 따라서 edgecolor (ec), linestyle (ls), linewidth (lw)가 적용됩니다.

  • 불필요한 axis도 지워버립시다. 명령은 똑같이 ax.axis(False)입니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    fig, ax = plt.subplots(figsize=(5, 5), 
                           constrained_layout=True,
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37))[:,:-9], 
                    df["y"].values.reshape((19, 37))[:,:-9], 
                    df["z"].values.reshape((19, 37))[:,:-9], 
                    ec="k", lw=0.2, ls=":",
                    alpha=0.3)
    ax.set_box_aspect((1, 1, 1))
    ax.axis(False)


  • 아까보다 한결 깔끔해 보입니다.

2.4. 면 색깔 조정

  • 면 색깔을 지정하는 매개변수는 color입니다.

  • colors="g"처럼 색상을 의미하는 약어나 숫자를 넣으면 적용됩니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    fig, ax = plt.subplots(figsize=(5, 5), 
                           constrained_layout=True,
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37))[:,:-9], 
                    df["y"].values.reshape((19, 37))[:,:-9], 
                    df["z"].values.reshape((19, 37))[:,:-9], 
                    ec="k", lw=0.2, ls=":",
                    color="g",
                    alpha=0.3)
    ax.set_box_aspect((1, 1, 1))
    ax.axis(False)


  • 조명 방향도 바꿀 수 있습니다.

  • matplotlib.colors의 LightSource 클래스를 사용해 조명 방향을 지정합니다.

  • 두 개의 인자로 방위각과 극고도각을 도(degree) 단위로 입력합니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    from matplotlib.colors import LightSource

    fig, axs = plt.subplots(ncols=3,
                            figsize=(15, 5), 
                            constrained_layout=True,
                            subplot_kw={"projection":"3d"})

    lightsources = [LightSource(30, 30), LightSource(-30, 60), LightSource(0, 0)]
    titles = ["azi: 30, polar: 30", "azi: -30, polar: 60", "azi: 0, polar: 0"]
    for ax, ls, title in zip(axs, lightsources, titles):
        ax.plot_surface(df["x"].values.reshape((19, 37))[:,:-9], 
                        df["y"].values.reshape((19, 37))[:,:-9], 
                        df["z"].values.reshape((19, 37))[:,:-9], 
                        ec="none", lw=0, ls="-",
                        color="w", lightsource=ls,
                        alpha=1)
        ax.set_title(title, fontsize="large")
        ax.set_box_aspect((1, 1, 1))
        ax.axis(False)


  • 멋진 그라데이션을 입히고 싶다면 cmap 매개변수를 사용할 수 있습니다.

  • z축 방향 값에 따른 그라데이션이 매겨집니다.

  • Matplotlib이 제공하는 gradation 이름을 집어넣습니다.

  • 다만 cmap과 lightsource는 함께 쓰일 수 없으니 유의해야 합니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    fig, ax = plt.subplots(figsize=(5, 5), 
                           constrained_layout=True,
                           subplot_kw={"projection":"3d"})
    ax.plot_surface(df["x"].values.reshape((19, 37))[:,:-9], 
                    df["y"].values.reshape((19, 37))[:,:-9], 
                    df["z"].values.reshape((19, 37))[:,:-9], 
                    ec="k", lw=0.2, ls=":",
                    cmap="inferno",
                    alpha=0.3)
    ax.set_box_aspect((1, 1, 1))
    ax.axis(False)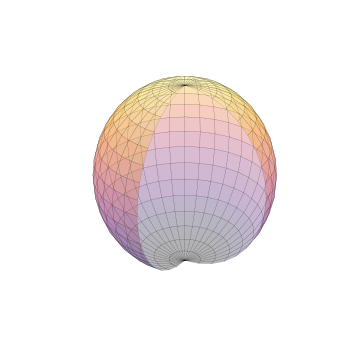


3. 응용

3.1. 구와 반구

stackoverflow: Axes3D 여백 없애기

  • 구와 반구를 동시에 그려봅니다.

  • 구는 위에서 만든 코드를 그대로 사용하면 되고,

  • 반구는 극고도각을 절반만 사용하면 됩니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    fig, axs = plt.subplots(ncols=2, 
                            figsize=(10, 5), 
                            constrained_layout=True, 
                            subplot_kw={"projection":"3d"})

    # sphere
    axs[0].plot_surface(df["x"].values.reshape((19, 37)), 
                        df["y"].values.reshape((19, 37)), 
                        df["z"].values.reshape((19, 37)), 
                        cmap="viridis", 
                        alpha=0.3)
    axs[0].set_box_aspect((1, 1, 1))
    axs[0].set_title("sphere", pad=12)

    # hemisphere
    axs[1].plot_surface(df["x"].iloc[:370].values.reshape((10, 37)), 
                        df["y"].iloc[:370].values.reshape((10, 37)), 
                        df["z"].iloc[:370].values.reshape((10, 37)), 
                        cmap="viridis", 
                        alpha=0.3)

    axs[1].set_box_aspect((1, 1, 0.5))
    axs[1].set_title("hemisphere", pad=12)

    for ax in axs:
        ax.set_xlabel("X")
        ax.set_ylabel("Y")
        ax.set_zlabel("Z")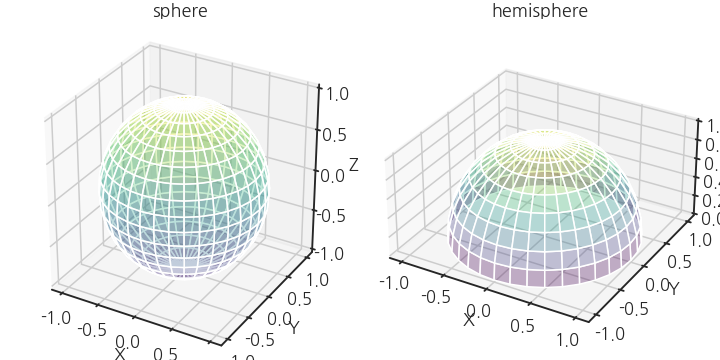


  • X, Y, Z축 범위가 -1~1을 약간 벗어나 있습니다.

  • matplotlib 기본 설정 문제입니다.

  • 이를 해결하려면 위 코드에서 fig, axs를 생성한 뒤에 짧은 코드를 추가합니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    from mpl_toolkits.mplot3d.axis3d import Axis
    if not hasattr(Axis, "_get_coord_info_old"):
        def _get_coord_info_new(self, renderer):
            mins, maxs, centers, deltas, tc, highs = self._get_coord_info_old(renderer)
            mins += deltas / 4
            maxs -= deltas / 4
            return mins, maxs, centers, deltas, tc, highs
        Axis._get_coord_info_old = Axis._get_coord_info  
        Axis._get_coord_info = _get_coord_info_new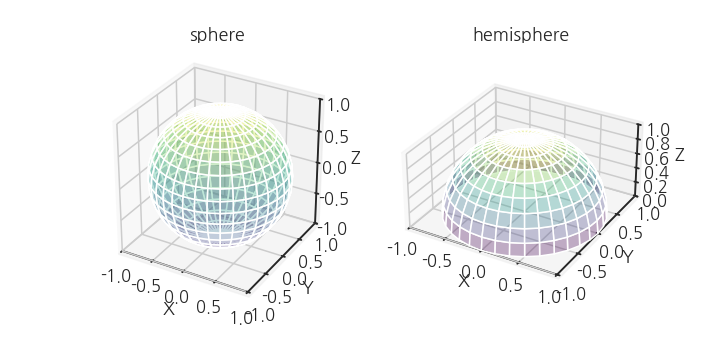


  • 동서남북, 그리고 상하를 잇는 수직선을 그립니다.

  • 좌표 원점이라고 봐도 됩니다.

  • 여기서 한 가지 주의할 점이 있습니다.

  • matplotlib이 3D 도형과 2D 도형의 위치관계를 깔끔하기 처리하지 못합니다.

  • 3D 도형에 가려질 부분과 가려지지 않을 부분을 따로 그리고 표현해줘야 합니다.

  • 동서남북을 나타내는 N, E, W, S도 적당한 위치에 넣어줍니다.

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    fig, axs = plt.subplots(ncols=2, 
                            figsize=(10, 5), 
                            subplot_kw={"projection":"3d"})

    # Axes3D 딱 붙이기
    # https://stackoverflow.com/questions/16488182/removing-axes-margins-in-3d-plot
    from mpl_toolkits.mplot3d.axis3d import Axis
    if not hasattr(Axis, "_get_coord_info_old"):
        def _get_coord_info_new(self, renderer):
            mins, maxs, centers, deltas, tc, highs = self._get_coord_info_old(renderer)
            mins += deltas / 4
            maxs -= deltas / 4
            return mins, maxs, centers, deltas, tc, highs
        Axis._get_coord_info_old = Axis._get_coord_info  
        Axis._get_coord_info = _get_coord_info_new

    # sphere
    axs[0].plot_surface(df["x"].values.reshape((19, 37)), 
                        df["y"].values.reshape((19, 37)), 
                        df["z"].values.reshape((19, 37)), 
                        cmap="viridis", ec="k", lw=0.1, 
                        alpha=0.3)
    axs[0].set_box_aspect((1, 1, 1))
    axs[0].set_title("sphere", pad=12)

    # hemisphere
    axs[1].plot_surface(df["x"].iloc[:370].values.reshape((10, 37)), 
                        df["y"].iloc[:370].values.reshape((10, 37)), 
                        df["z"].iloc[:370].values.reshape((10, 37)), 
                        cmap="viridis", ec="k", lw=0.1, 
                        alpha=0.3)

    axs[1].set_box_aspect((1, 1, 0.5))
    axs[1].set_title("hemisphere", pad=12)

    for ax in axs:
        ax.set_xlabel("X")
        ax.set_ylabel("Y")
        ax.set_zlabel("Z")
        ax.view_init(azim=235)
        # make margins
        ax.margins(0)
        # center axis
        zmin = -1 if ax == axs[0] else 0
        ax.plot([-1.1, 1.1], [0, 0], [0, 0], c="k", zorder=-10)
        ax.plot([0, 0, 0], [-1.1, 1.1, 0], c="k", zorder=-10)
        ax.plot([0, 0], [0, 0], [zmin, 1], c="k", zorder=-10)
        ax.plot([0, 0], [0, 0], [1, 1.1], c="k", zorder=3)
        
        if ax == axs[0]:
            ax.plot([-1, -1.1], [0, 0], [0, 0], c="k", zorder=3)
            ax.plot([0, 0], [-1, -1.1], [0, 0], c="k", zorder=3)
         
        # 동서남북 표시
        font_text = {"fontweight":"bold", "fontsize":15, "ha":"center", "va":"center"}
        ax.text(-1.4, 0, 0, "W", transform=ax.transData, fontdict=font_text)
        ax.text(1.4, 0, 0, "E", transform=ax.transData, fontdict=font_text)
        ax.text(0, 1.4, 0, "N", transform=ax.transData, fontdict=font_text, zorder=-10)
        ax.text(0, -1.4, 0, "S", transform=ax.transData, fontdict=font_text)
        ax.axis(False)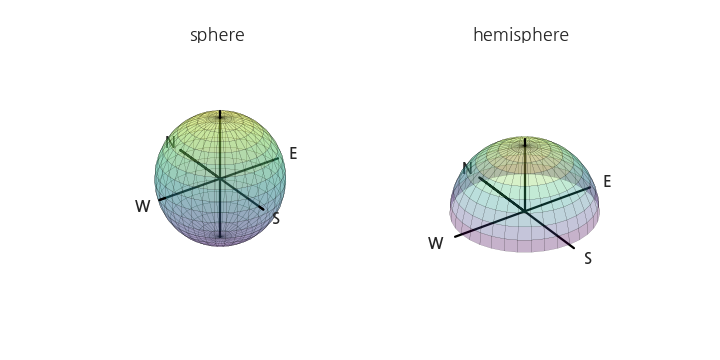


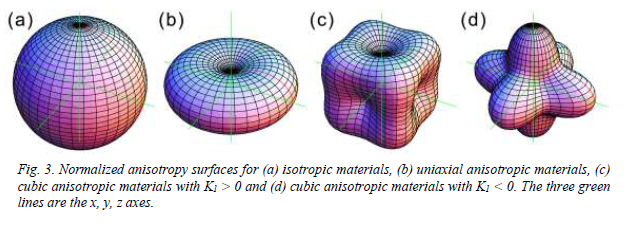
3.2. magnetocrystalline anisotropy

wikipedia: magnetocrystalline anisotropy

  • 결정자기이방성(magnetocrystalline anisotropy)이라는 말을 들어보신 분은 거의 없으실 겁니다.
  • 자성(magnetism)을 공부할 때 나오는 용어인데, 방위에 따라 다른 에너지라고 대충 넘어가셔도 좋습니다.
  • 중요한 것은 이번엔 구나 반구가 아니라 울퉁불퉁한 모양을 만들 것이라는 점입니다.
  • 원리는 간단합니다.
  • 이 글의 처음에서 구면좌표계는 다음과 같은 식으로 표현된다고 했습니다.

$$
\begin{aligned}
x &= r \cos{\varphi} \sin{\theta}\\
y &= r \sin{\varphi} \sin{\theta}\\
z &= r \cos{\theta}
\end{aligned}$$

  • 앞에서는 $r = 1$로 두었지만, 여기서는 $r = f(\varphi, \theta)$입니다.
  • 방위각과 극고도각을 이용해서 물질마다 다르게 r을 정의합니다.
  • 모양이 울퉁불퉁한만큼 아까 10도 단위로 쪼갠 공간을 이번엔 5도 단위로 쪼갭니다.
  • 자세한 설명은 생략하고 결과 그림과 코드만 간략히 보여드리겠습니다.

  • 5도 단위로 공간 분할

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    # angles
    polars = np.linspace(0, 179, 37)
    azimuths = np.linspace(0, 360, 73)

    # points
    from itertools import product

    df = pd.DataFrame(product(polars, azimuths), columns=["azi", "polar"])
    df["x"] = df.apply(lambda x: np.cos(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
    df["y"] = df.apply(lambda x: np.sin(np.deg2rad(x[1]))*np.sin(np.deg2rad(x[0])), axis=1)
    df["z"] = df.apply(lambda x: np.cos(np.deg2rad(x[0])), axis=1)

  • 방향에 따른 $r$ 계산: 자기이방성 에너지

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    # 자기이방성 계수 K1, K2
    K1_Co = 45
    K2_Co = 15

    K1_Fe = 4.8
    K2_Fe = 0.5

    K1_Ni = -0.5 
    K2_Ni = -0.2

    # 방향에 따른 자기이방성 에너지 계산.
    # 그림을 그리는 것이 목적이므로 보기 좋도록 적절히 스케일링
    def calc_uni(K1, K2, df):
        return K1*(df["x"]**2 + df["y"]**2)

    def calc_cubic(K1, K2, df):
        return K1*(df["x"]**2 * df["y"]**2 + \
                   df["y"]**2 * df["z"]**2 + \
                   df["z"]**2 * df["x"]**2) + \
               K2*(df["x"]**2 * df["y"]**2 * df["z"]**2)

    df["E_Co"] = df.apply(lambda x: calc_uni(K1_Co, K2_Co, x), axis=1) + 1
    df["E_Fe"] = df.apply(lambda x: calc_cubic(K1_Fe, K2_Fe, x), axis=1) + 1
    df["E_Ni"] = df.apply(lambda x: calc_cubic(K1_Ni, K2_Ni, x), axis=1)*3 +1

    # 극좌표계를 직교좌표계로 변환
    df["x_Co"] = df["E_Co"] * df["x"]
    df["y_Co"] = df["E_Co"] * df["y"]
    df["z_Co"] = df["E_Co"] * df["z"]

    df["x_Fe"] = df["E_Fe"] * df["x"]
    df["y_Fe"] = df["E_Fe"] * df["y"]
    df["z_Fe"] = df["E_Fe"] * df["z"]

    df["x_Ni"] = df["E_Ni"] * df["x"]
    df["y_Ni"] = df["E_Ni"] * df["y"]
    df["z_Ni"] = df["E_Ni"] * df["z"]

  • 세 가지 물질(Co, Fe, Ni)의 자기이방성 에너지 시각화

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    fig, axs = plt.subplots(ncols=3, 
                            figsize=(15, 6), 
                           constrained_layout=True,
                            subplot_kw={"projection":"3d"})
    for ax, mat in zip(axs, ["Co", "Fe", "Ni"]):
        ax.plot_surface(df[f"x_{mat}"].values.reshape((37, 73))[:,:-19], 
                        df[f"y_{mat}"].values.reshape((37, 73))[:,:-19], 
                        df[f"z_{mat}"].values.reshape((37, 73))[:,:-19], 
                        ec="k", lw=0.2,
                        color="w", lightsource=LightSource(0, 10),
                        alpha=1)
        ax.plot(df[f"x_{mat}"].values.reshape((37, 73))[:,-20], 
                df[f"y_{mat}"].values.reshape((37, 73))[:,-20], 
                df[f"z_{mat}"].values.reshape((37, 73))[:,-20], 
                c="k", alpha=1)
        ax.plot(df[f"x_{mat}"].values.reshape((37, 73))[:,0], 
                df[f"y_{mat}"].values.reshape((37, 73))[:,0], 
                df[f"z_{mat}"].values.reshape((37, 73))[:,0], 
                c="k", alpha=1)
        ax.set_box_aspect((1, 1, 1))
        ax.axis(False)
        ax.set_title(mat, fontsize="xx-large")
        
    fig.suptitle("crystalline anisotropy energy surface\n", 
                 color="blue", fontsize="xx-large")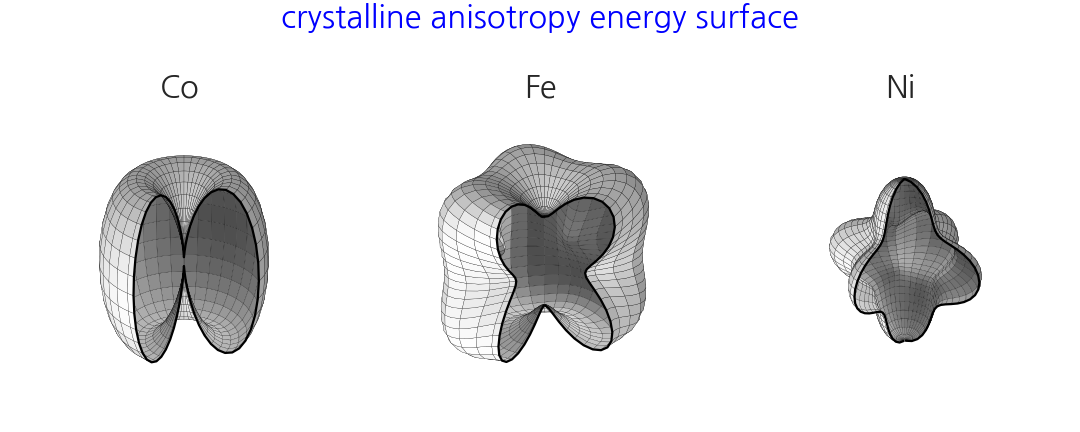


  • 제 박사학위 주제와 밀접한 그림입니다.

  • 교과서 그림을 모방해 학위논문(2011)에도 같은 그림을 그려서 넣었습니다.

  • mathematica를 사용해서 그린 그림입니다.



도움이 되셨나요? 카페인을 투입하시면 다음 포스팅으로 변환됩니다

Share